Page 138 - https://lacatedra.com/

Cuadernillo de actividades para el desarrollo de habilidades matemáticas. 1º secundaria.

S Si ig gn ni if fi ic ca ad do o y y u us so o d de e l la as s l li it te er ra al le es s. .

R R Re e el l la a ac c ci i ió ó ón n n f f fu u un n nc c ci i io o on n na a al l l. . .

Vínculos entre representaciones de proporcionalidad directa con gráficas, tablas y expresiones
algebraicas.

Para determinar si una relación es de proporcionalidad directa se puede hacer lo siguiente:
A partir de la relación, construir una tabla para encontrar algunos valores y determinar si esta tabla es
de proporcionalidad directa. A partir de la tabla, construir la gráfica y determinar si los puntos están en
una línea recta.

Puede suceder que distintas situaciones proporcionales tengan la misma expresión algebraica
asociada.

Por ejemplo:
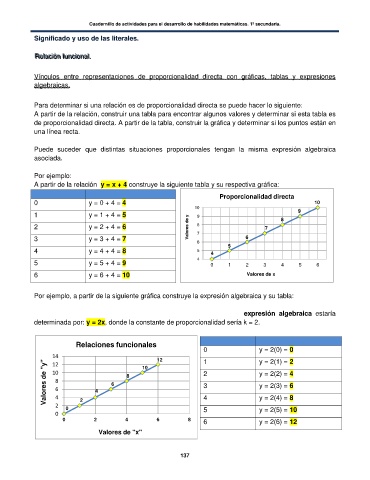
A partir de la relación y = x + 4 construye la siguiente tabla y su respectiva gráfica:
Valores de “x” Valores de “y” si y = x + 4 Proporcionalidad directa
0 y = 0 + 4 = 4 10
10
1 y = 1 + 4 = 5 9 8 9
2 y = 2 + 4 = 6 Valores de y 8 7
3 y = 3 + 4 = 7 7 6
6
5
4 y = 4 + 4 = 8 5 4

5 y = 5 + 4 = 9 4 0 1 2 3 4 5 6
6 y = 6 + 4 = 10 Valores de x

Por ejemplo, a partir de la siguiente gráfica construye la expresión algebraica y su tabla:
Aquí observamos que por cada valor de “x” que se aumenta, los valores de “y” también aumentan en
2 unidades, es decir, “y” aumenta al doble de “x”, por lo que la expresión algebraica estaría
determinada por: y = 2x, donde la constante de proporcionalidad sería k = 2.

Valores de “x” Valores de “y” si y = 2x
Relaciones funcionales 0 y = 2(0) = 0
14 12 1 y = 2(1) = 2
12 10
10 8 2 y = 2(2) = 4
Valores de "y" 8 6 3 y = 2(3) = 6
6 4
4 2 4 y = 2(4) = 8
2 0 5 y = 2(5) = 10
0
0 2 4 6 8 6 y = 2(6) = 12
Valores de "x"

137